Construction of an FA from an RE

We can use Thompson's Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.

Some basic RA expressions are the following −

Case 1 − For a regular expression ‘a’, we can construct the following FA −

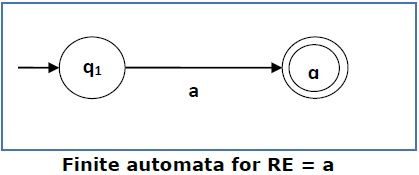
Case 2 − For a regular expression ‘ab’, we can construct the following FA −

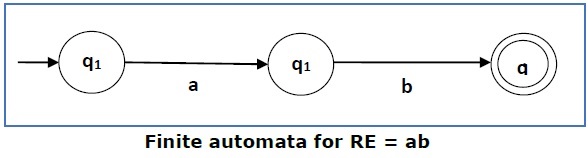
Case 3 − For a regular expression (a+b), we can construct the following FA −

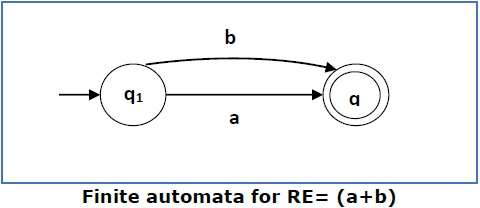
Case 4 − For a regular expression (a+b)*, we can construct the following FA −

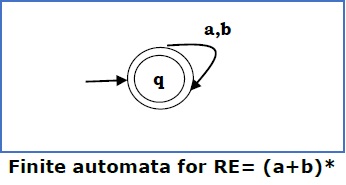
Method

Step 1	Construct an NFA with Null moves from the given regular expression.
Step 2	Remove Null transition from the NFA and convert it into its equivalent DFA.

Problem

Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0

Solution

We will concatenate three expressions "1", "(0 + 1)*" and "0"

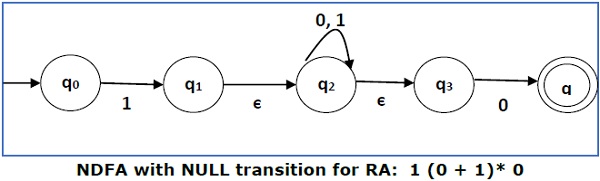
Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

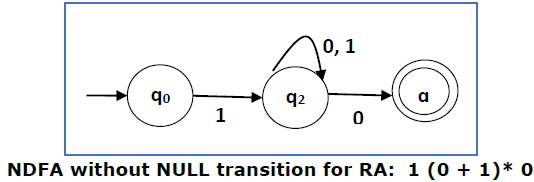
It is an NDFA corresponding to the RE: 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA